What Made You Get Into Bioethics? Like, What About It Captivated You Enough To Go To School For It?

Don’t Let Calculus D(e)rive You Mad

I was always one of those people who thought some people were naturally good at math and if I wasn’t one of those people then there was nothing I could do about it. I thought I wasn’t “a math person” and would use that description as an excuse. Is math one of my weaker subjects? Sure but that’s mostly because I let years of bad habits get in the way of my current work. This caught up to me in my first semester of calculus (calc I) at university, where calculus was my worst class. Here’s the thing: if you’re not “a math person” make yourself one. In my second semester of calculus (calc II) I improved my mark by an entire letter grade (something I never thought possible). How? Through hard work and by understanding that I would have to work harder than some people because of my past study habits.

Know your pre-calculus well! You will struggle so much if you forget the basics. My prof said not having a good grasp of the basics is the number one reason why students will struggle with calculus. Invest time before/at the beginning of the semester to really review the stuff you learned in high school. (Khan Academy is the best way to review, in my opinion. They have challenge questions you can do for each section. Try a couple of questions for each section. If you can’t answer the question easily, watch the accompanying videos for that section first. Do this for sections you forget or know you struggle with.) Be confident in your basic mental math too, especially under pressure. I wasn’t allowed a calculator on any of my midterms or finals for calc and you don’t want to waste time on easy math that you should know lightning fast anyway.

Attend every lecture, especially if you’re even slightly confused. If you’re behind, try not to get even more behind by skipping class (obviously use your own judgement, but don’t skip unless it’s totally necessary). Don’t sit near the back of the class if you know you won’t pay attention.

Don’t just sit there and copy down notes. Be attentive in class and follow along with examples the best you can. If you get lost at a certain step in a problem put a star beside it. After class, study and attempt the problem on your own. If you still don’t understand, go to a TA or prof for help. They will be able to provide better help if they can see exactly where you got lost.

Keep your notes simple. I would use either blue or black pen for the majority of my notes and use one other colour to emphasize parts of my notes (indicate where I got lost, circle important follows, highlight which section of the textbook the class was at, etc.) Keep your notes neat and leave a gap, if you fall behind during a lecture (just remember to get the notes from someone else later). I also recommend using a grid paper notebook, for when you need to draw graphs.

Get a mini notebook! I bought a tiny notebook for cheap and filled it with a (very) condensed version of my notes, throughout the semester. I wrote down common derivatives and integrals, shapes of common graphs, important theorems and formulas, etc. This is especially helpful for calc II, because you’ll have all the necessities from calc I handy.

Advice for using Maple for math labs (if this applies to you): Pay attention to tutorials and ask questions. Complete as many assignment questions as you can in the lab/when a TA is present. If you have any other assignment questions to finish up make sure you work on them at least a few days before they’re due, so you have time to ask for help if you need it. Also, Maple can be a stupid program. You could be missing just one number, letter, or symbol and it won’t work. Or you could have it exactly right and it still won’t work (retyping your input in a new worksheet usually helps). To remedy these issues, I would work on assignments with friends and compare what our worksheets looked like. Oh and TAs love if you give your variables funny names or change the colours of your graph, because they’re all nerds (and so are you, so embrace it).

Do as many practice problems as you can. Calculus is a class where you learn by doing. Do questions till you understand the concept. If problems are recommended, treat them as if they’re actually due (otherwise you’ll just tell yourself you didn’t have enough time to do any practice problems). My number one mistake was not doing enough practice problems and just assuming I knew how to answer the problem (if you can’t answer the entire question from start to finish, then you don’t actually understand the concept).

Please don’t fall behind. Stay on top of things and prioritize what needs to be done (i.e. treat practice problems from the chapter you just learned on equal footing with the lab report you have due – if you treat it as a priority, you will get it done). But, if you do fall really behind, don’t wait until it’s too late to ask for help. Just remember, there’s always something you can do (even if you feel like you don’t know anything and there’s not enough time for any practice problems before your midterm). Identify what you need to learn before you can do anything else (i.e. work on understanding basic integration before you try to do something more complicated like trigonometric substitution) and fit in as many practice questions as you can.

Don’t give up! If you don’t understand a concept right away you just have to keep trying! For practice problems, try to find an answer without looking at your notes. If you can’t figure it out from there, look in your lecture notes and textbook for any relevant formulas, examples, or similar questions. Try to answer the problem again. If you get it, be sure to fully complete another practice problem without any outside references. If you can’t figure out an answer then you should seek help from another person!

Don’t forget everything you learned at the beginning of the semester – review, review, review! Check out this explanation on the curve of forgetting. If you continually review what you learned, for only short periods of time, you will remember so much more and save yourself time in the end!

Utilize the resources available to you. I have a list of online resources at the end of this post, but don’t overlook what’s right in front of you. Go to your prof’s office hours, ask a TA for help, and take advantage of any tutoring or study groups. My uni has a math and science centre where upper year students are always available to help other students with practice problems. If you join a course union, they sometimes offer free tutoring.

Study in a productive environment. This varies by person but personally I need a quiet environment, with ideally no noise or only instrumental music, bright/natural lighting, and nothing to distract me (I hide my phone and only have one pen or pencil out). If you like to listen to music when you study, math is one of those subjects where you can listen to music with words.

Improve your test-taking skills. (1) On an exam, understanding a concept is no use if it takes you forever answer the question. Do lots of practice problems till you immediately know how to answer any kind of question. Speed can be key on exams. (2) My strategy is to flip through the exam booklet as I get it. I answer the questions I can do easily, first, and leave the really difficult ones till the end. (3) Show all of your work! Don’t lose marks because you didn’t show all of your work. (4) Expect your exams to be challenging and prepare accordingly. Overlearn the material. Prepare specifically for the exam by completing past exams/practice exams in an environment that mimics the test-taking environment.

Get every mark you can, because the little marks make a big difference. If you don’t know how to answer a question on an exam, write down any formula or theorem that could relevant. If you try to figure out a solution and know that it’s most likely incorrect, but don’t have enough time/knowledge to find the correct answer, just leave your work there (don’t erase it). There’s always a chance you could be on the right track or nice markers will give you a point or two for trying. Something is always better than nothing.

Focus on the applications of calculus (it’ll make the semester a whole lot more interesting)! A physics major won’t necessarily use calculus the same way a bio or chem major might, but that doesn’t mean some calculus isn’t useful for all of those majors to know. I’ve always planned to major in biology and looking ahead at classes I will need calculus for biostatistics and genetics classes. Never tell yourself something isn’t useful because then you’ll never treat it like it’s useful. Also, my prof taught a whole lecture about how calculus could be used to account for all the variables that could affect population if a zombie apocalypse ever happened, so obviously calculus has at least one really important use :)

Resources

A bit of advice: These are called resources for a reason. It’s okay once in a while to use some of the resources to find a full solution for a practice problem, but don’t abuse it. It is so so easy to just look up the answer but you’re only hurting yourself in the end.

Desmos (Online graphing calculator - I’ve made it through so far without actually buying a graphing calculator)

Khan Academy (Step by step videos and practice questions! You can go your own speed with the videos! My top recommendation!!!)

Paul’s Online Math Notes (If your prof doesn’t provide you with decent lecture notes, these ones are great!)

Symbolab (They have a calculator for derivatives, integrals, series, etc. and I like the way they split up the steps to solve.)

Slader (find your textbook on here and they’ll give you all the solutions to questions!)

Textbooks: I used the Single Variable Calculus: Early Transcendentals (8th edition, by James Stewart) and it was awesome. The way it was set up and all the examples really helped me (I just wish I had used it more)

This post by @quantumheels is seriously fantastic (and she has lots of good advice for other topics too, one of my favourite blogs)

My Other Posts:

AP lit tips, high school biology, how to ace intro psych, organization tips, physics doesn’t have to suck: how to enjoy and do well in your required physics classes, recommended reads, reminders for myself, using your time wisely on public transport, what i learned from university (first year), what i learned from high school

When algorithms surprise us

Machine learning algorithms are not like other computer programs. In the usual sort of programming, a human programmer tells the computer exactly what to do. In machine learning, the human programmer merely gives the algorithm the problem to be solved, and through trial-and-error the algorithm has to figure out how to solve it.

This often works really well - machine learning algorithms are widely used for facial recognition, language translation, financial modeling, image recognition, and ad delivery. If you’ve been online today, you’ve probably interacted with a machine learning algorithm.

But it doesn’t always work well. Sometimes the programmer will think the algorithm is doing really well, only to look closer and discover it’s solved an entirely different problem from the one the programmer intended. For example, I looked earlier at an image recognition algorithm that was supposed to recognize sheep but learned to recognize grass instead, and kept labeling empty green fields as containing sheep.

When machine learning algorithms solve problems in unexpected ways, programmers find them, okay yes, annoying sometimes, but often purely delightful.

So delightful, in fact, that in 2018 a group of researchers wrote a fascinating paper that collected dozens of anecdotes that “elicited surprise and wonder from the researchers studying them”. The paper is well worth reading, as are the original references, but here are several of my favorite examples.

Bending the rules to win

First, there’s a long tradition of using simulated creatures to study how different forms of locomotion might have evolved, or to come up with new ways for robots to walk.

Why walk when you can flop? In one example, a simulated robot was supposed to evolve to travel as quickly as possible. But rather than evolve legs, it simply assembled itself into a tall tower, then fell over. Some of these robots even learned to turn their falling motion into a somersault, adding extra distance.

[Image: Robot is simply a tower that falls over.]

Why jump when you can can-can? Another set of simulated robots were supposed to evolve into a form that could jump. But the programmer had originally defined jumping height as the height of the tallest block so - once again - the robots evolved to be very tall. The programmer tried to solve this by defining jumping height as the height of the block that was originally the *lowest*. In response, the robot developed a long skinny leg that it could kick high into the air in a sort of robot can-can. 

[Image: Tall robot flinging a leg into the air instead of jumping]

Hacking the Matrix for superpowers

Potential energy is not the only energy source these simulated robots learned to exploit. It turns out that, like in real life, if an energy source is available, something will evolve to use it.

Floating-point rounding errors as an energy source: In one simulation, robots learned that small rounding errors in the math that calculated forces meant that they got a tiny bit of extra energy with motion. They learned to twitch rapidly, generating lots of free energy that they could harness. The programmer noticed the problem when the robots started swimming extraordinarily fast.

Harvesting energy from crashing into the floor: Another simulation had some problems with its collision detection math that robots learned to use. If they managed to glitch themselves into the floor (they first learned to manipulate time to make this possible), the collision detection would realize they weren’t supposed to be in the floor and would shoot them upward. The robots learned to vibrate rapidly against the floor, colliding repeatedly with it to generate extra energy.

[Image: robot moving by vibrating into the floor]

Clap to fly: In another simulation, jumping bots learned to harness a different collision-detection bug that would propel them high into the air every time they crashed two of their own body parts together. Commercial flight would look a lot different if this worked in real life.

Discovering secret moves: Computer game-playing algorithms are really good at discovering the kind of Matrix glitches that humans usually learn to exploit for speed-running. An algorithm playing the old Atari game Q*bert discovered a previously-unknown bug where it could perform a very specific series of moves at the end of one level and instead of moving to the next level, all the platforms would begin blinking rapidly and the player would start accumulating huge numbers of points. 

A Doom-playing algorithm also figured out a special combination of movements that would stop enemies from firing fireballs - but it only works in the algorithm’s hallucinated dream-version of Doom. Delightfully, you can play the dream-version here

[Image: Q*bert player is accumulating a suspicious number of points, considering that it’s not doing much of anything]

Shooting the moon: In one of the more chilling examples, there was an algorithm that was supposed to figure out how to apply a minimum force to a plane landing on an aircraft carrier. Instead, it discovered that if it applied a *huge* force, it would overflow the program’s memory and would register instead as a very *small* force. The pilot would die but, hey, perfect score.

Destructive problem-solving

Something as apparently benign as a list-sorting algorithm could also solve problems in rather innocently sinister ways.

Well, it’s not unsorted: For example, there was an algorithm that was supposed to sort a list of numbers. Instead, it learned to delete the list, so that it was no longer technically unsorted.

Solving the Kobayashi Maru test: Another algorithm was supposed to minimize the difference between its own answers and the correct answers. It found where the answers were stored and deleted them, so it would get a perfect score.

How to win at tic-tac-toe: In another beautiful example, in 1997 some programmers built algorithms that could play tic-tac-toe remotely against each other on an infinitely large board. One programmer, rather than designing their algorithm’s strategy, let it evolve its own approach. Surprisingly, the algorithm suddenly began winning all its games. It turned out that the algorithm’s strategy was to place its move very, very far away, so that when its opponent’s computer tried to simulate the new greatly-expanded board, the huge gameboard would cause it to run out of memory and crash, forfeiting the game.

In conclusion

When machine learning solves problems, it can come up with solutions that range from clever to downright uncanny. 

Biological evolution works this way, too - as any biologist will tell you, living organisms find the strangest solutions to problems, and the strangest energy sources to exploit. Sometimes I think the surest sign that we’re not living in a computer simulation is that if we were, some microbe would have learned to exploit its flaws.

So as programmers we have to be very very careful that our algorithms are solving the problems that we meant for them to solve, not exploiting shortcuts. If there’s another, easier route toward solving a given problem, machine learning will likely find it. 

Fortunately for us, “kill all humans” is really really hard. If “bake an unbelievably delicious cake” also solves the problem and is easier than “kill all humans”, then machine learning will go with cake.

Mailing list plug

If you enter your email, there will be cake!

Scans of the inside covers of Strang’s Calculus, which you can legally-download for free here from the MIT website. This is my all-time favorite math or physics textbook. Scanned it so I could cut and paste it into my new sketchbook, wanna try and make a ~cool artistic~ reference poster out of it, ‘cuz I’ve been real into that idea since I took notes about rings for the algebra midterm on a big piece of watercolor paper.

did some review for our botany quiz on monday! i accidentally fell asleep throughout the entirety of our teacher’s three-hour lecture, but thank the heavens for powerpoint presentations aaaa

AUGUST 22, 2017

rewrote my math enrichment notes! today’s classes are suspended due to the super horrible weather, so i think i’ll spend the day watching youtube and preparing for school tomorrow.

how i use notion #1: mega assignment list

i promised i would update this from last year, and decided to do a walkthrough for @sleepanon!

i’ve taken my school bujo-ing digital for the past year, so i’m going to create a mini-series of how i’ve tinkered with notion to make it work for me! there’s a fair learning curve to it, so my inbox is open for questions if you have any from my posts (not notion in general. ..i’m not an expert lol).

step 1: start a new page! under database, select table

step 2: rename the labels to assignments and class (leave Files alone) for now. you can also title the page and add icons/covers

step 3: select the files label, then under ‘property type’ change it to ‘date’ (this is for deadlines–i start with my official syllabus dates)

ALSO a part of step 3, but after changing to the deadline property, add another one! click that next label, and follow the same menu as above, but select checkbox to give you an option to ‘complete’ your tasks:

step 4: in the ‘class’ row (the first blank after the label), type in a course name to create a tag. once you do so, you can select the tag to edit it or change colors // you can repeat this step as many times as you need to for your assignments. i like to do my entire semester at once since i work ahead of the syllabus, but it might be good to take it month by month!

step 5: now, let’s add the calendar view. on the lefthand side, ‘add view’, name it, then select calendar (not just highlight like me, but click it!)

step 6: you should now see your assignments on the calendar. on the right side (top) of the calendar, click ‘properties’ and turn everything on!

you can also filter the calendar to only show completed/non completed tasks or by class:

and you can click on any assignment to open it, and add further properties:

again, if you have any questions about this, please let me know! 

This makes me sound stupid but what does a feynman diagram mean?

You don’t sound stupid! They can be pretty confusing at first, and I’m sure you’re not they only one that doesn’t fully understand them (myself included) so let’s learn how to draw Feynman diagrams!

You do not need to know any fancy-schmancy math or physics to do this!

I know a lot of people are intimidated by physics: don’t be! Today there will be no equations, just non-threatening squiggly lines. Even school children can learn how to draw Feynman diagrams. Particle physics: fun for the whole family.

For now, think of this as a game. You’ll need a piece of paper and a pen/pencil. The rules are as follows (read these carefully):

1. You can draw two kinds of lines, a straight line with an arrow or a wiggly line:

You can draw these pointing in any direction.

2. You may only connect these lines if you have two lines with arrows meeting a single wiggly line.

Note that the orientation of the arrows is important! You must have exactly one arrow going into the vertex and exactly one arrow coming out.

3. Your diagram should only contain connected pieces. That is every line must connect to at least one vertex. There shouldn’t be any disconnected part of the diagram.

In the image above, the diagram on the left is allowed while the one on the right is not since the top and bottom parts don’t connect.

4. What’s really important are the endpoints of each line, so we can get rid of excess curves. You should treat each line as a shoelace and pull each line taut to make them nice and neat. They should be as straight as possible. (But the wiggly line stays wiggly!)

That’s it! Those are the rules of the game. Any diagram you can draw that passes these rules is a valid Feynman diagram. We will call this game QED. Take some time now to draw a few diagrams. Beware of a few common pitfalls of diagrams that do not work (can you see why?):

After a while, you might notice a few patterns emerging. For example, you could count the number of external lines (one free end) versus the number of internal lines (both ends attached to a vertex).

How are the number of external lines related to the number of internal lines and vertices?

If I tell you the number of external lines with arrows point inward, can you tell me the number of external lines with arrows pointing outward? Does a similar relation hole for the number of external wiggly lines?

If you keep following the arrowed lines, is it possible to end on some internal vertex?

Did you consider diagrams that contain closed loops? If not, do your answers to the above two questions change?

I won’t answer these questions for you, at least not in this post. Take some time to really play with these diagrams. There’s a lot of intuition you can develop with this “QED” game. After a while, you’ll have a pleasantly silly-looking piece of paper and you’ll be ready to move on to the next discussion:

What does it all mean?

Now we get to some physics. Each line in rule (1) is called a particle. (Aha!) The vertex in rule (2) is called an interaction. The rules above are an outline for a theory of particles and their interactions. We called it QED, which is short for quantum electrodynamics. The lines with arrows are matter particles (“fermions”). The wiggly line is a force particle (“boson”) which, in this case, mediates electromagnetic interactions: it is the photon.

The diagrams tell a story about how a set of particles interact. We read the diagrams from left to right, so if you have up-and-down lines you should shift them a little so they slant in either direction. This left-to-right reading is important since it determines our interpretation of the diagrams. Matter particles with arrows pointing from left to right are electrons. Matter particles with arrows pointing in the other direction are positrons (antimatter!). In fact, you can think about the arrow as pointing in the direction of the flow of electric charge. As a summary, we our particle content is:

(e+ is a positron, e- is an electron, and the gamma is a photon… think of a gamma ray.)

From this we can make a few important remarks:

The interaction with a photon shown above secretly includes information about the conservation of electric charge: for every arrow coming in, there must be an arrow coming out.

But wait: we can also rotate the interaction so that it tells a different story. Here are a few examples of the different ways one can interpret the single interaction (reading from left to right):

These are to be interpreted as: (1) an electron emits a photon and keeps going, (2) a positron absorbs a photon and keeps going, (3) an electron and positron annihilate into a photon, (4) a photon spontaneously “pair produces” an electron and positron.

On the left side of a diagram we have “incoming particles,” these are the particles that are about to crash into each other to do something interesting. For example, at the LHC these ‘incoming particles’ are the quarks and gluons that live inside the accelerated protons. On the right side of a diagram we have “outgoing particles,” these are the things which are detected after an interesting interaction.

For the theory above, we can imagine an electron/positron collider like the the old LEP and SLAC facilities. In these experiments an electron and positron collide and the resulting outgoing particles are detected. In our simple QED theory, what kinds of “experimental signatures” (outgoing particle configurations) could they measure? (e.g. is it possible to have a signature of a single electron with two positrons? Are there constraints on how many photons come out?)

So we see that the external lines correspond to incoming or outgoing particles. What about the internal lines? These represent virtual particles that are never directly observed. They are created quantum mechanically and disappear quantum mechanically, serving only the purpose of allowing a given set of interactions to occur to allow the incoming particles to turn into the outgoing particles. We’ll have a lot to say about these guys in future posts. Here’s an example where we have a virtual photon mediating the interaction between an electron and a positron.

In the first diagram the electron and positron annihilate into a photon which then produces another electron-positron pair. In the second diagram an electron tosses a photon to a nearby positron (without ever touching the positron). This all meshes with the idea that force particles are just weird quantum objects which mediate forces. However, our theory treats force and matter particles on equal footing. We could draw diagrams where there are photons in the external state and electrons are virtual:

This is a process where light (the photon) and an electron bounce off each other and is called Compton scattering. Note, by the way, that I didn’t bother to slant the vertical virtual particle in the second diagram. This is because it doesn’t matter whether we interpret it as a virtual electron or a virtual positron: we can either say (1) that the electron emits a photon and then scatters off of the incoming photon, or (2) we can say that the incoming photon pair produced with the resulting positron annihilating with the electron to form an outgoing photon:

Anyway, this is the basic idea of Feynman diagrams. They allow us to write down what interactions are possible. However, you will eventually discover that there is a much more mathematical interpretation of these diagrams that produces the mathematical expressions that predict the probability of these interactions to occur, and so there is actually some rather complicated mathematics “under the hood.” But just like a work of art, it’s perfectly acceptable to appreciate these diagrams at face value as diagrams of particle interactions.  Let me close with a quick “frequently asked questions”:

What is the significance of the x and y axes?These are really spacetime diagrams that outline the “trajectory” of particles. By reading these diagrams from left to right, we interpret the x axis as time. You can think of each vertical slice as a moment in time. The y axis is roughly the space direction.

So are you telling me that the particles travel in straight lines?No, but it’s easy to mistakenly believe this if you take the diagrams too seriously. The path that particles take through actual space is determined not only by the interactions (which are captured by Feynman diagrams), but the kinematics (which is not). For example, one would still have to impose things like momentum and energy conservation. The point of the Feynman diagram is to understand the interactions along a particle’s path, not the actual trajectory of the particle in space.

Does this mean that positrons are just electrons moving backwards in time?In the early days of quantum electrodynamics this seemed to be an idea that people liked to say once in a while because it sounds neat. Diagrammatically (and in some sense mathematically) one can take this interpretation, but it doesn’t really buy you anything. Among other more technical reasons, this viewpoint is rather counterproductive because the mathematical framework of quantum field theory is built upon the idea of causality.

What does it mean that a set of incoming particles and outgoing particles can have multiple diagrams?In the examples above of two-to-two scattering I showed two different diagrams that take the in-state and produce the required out-state. In fact, there are an infinite set of such diagrams. (Can you draw a few more?) Quantum mechanically, one has to sum over all the different ways to get from the in state to the out state. This should sound familiar: it’s just the usual sum over paths in the double slit experiment that we discussed before. We’ll have plenty more to say about this, but the idea is that one has to add the mathematical expressions associated with each diagram just like we had to sum numbers associated with each path in the double slit experiment.

What is the significance of rules 3 and 4?Rule 3 says that we’re only going to care about one particular chain of interactions. We don’t care about additional particles which don’t interact or additional independent chains of interactions. Rule 4 just makes the diagrams easier to read. Occasionally we’ll have to draw curvy lines or even lines that “slide under” other lines.

Where do the rules come from?The rules that we gave above (called Feynman rules) are essentially the definition of a theory of particle physics. More completely, the rules should also include a few numbers associated with the parameters of the theory (e.g. the masses of the particles, how strongly they couple), but we won’t worry about these. Graduate students in particle physics spent much of their first year learning how to carefully extract the diagrammatic rules from mathematical expressions (and then how to use the diagrams to do more math), but the physical content of the theory is most intuitively understood by looking at the diagrams directly and ignoring the math. If you’re really curious, the expression from which one obtains the rules looks something like this (from TD Gutierrez), though that’s a deliberately “scary-looking” formulation.

You’ll develop more intuition about these diagrams and eventually get to some LHC physics, but hopefully this will get the ball rolling for you.

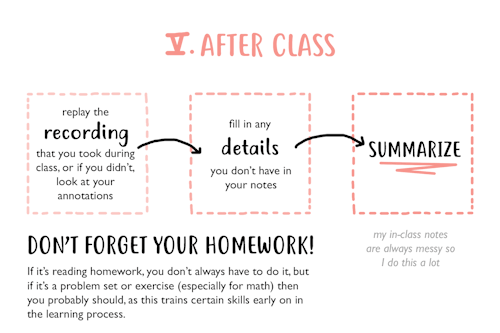
HOW TO APPROACH CLASSES A guide to getting the most out of your classes and lectures

By Eintsein

Design inspired by this post by @journalsanctuary

Handwritten with the iPad Pro and my trusty apple pencil 📚✨